Applications of Gauss's Law

Applying Gauss theorem, the expression for the electric field intensity at a point due to an infinitely long, thin, uniformly charged straight wire is

A hollow charged metal sphere has radius $r$. If the potential difference between its surface and a point at a distance $3r$ from the centre is$V$, then electric field intensity at a distance $3r$ is:

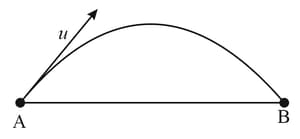
In the figure shown, there is a large sheet of charge of uniform surface charge density $\sigma$. A charge particle of charge $-q$ and mass $m$ is projected from a point $A$ on the sheet with a speed $u$ with angle of projection such that it lands at maximum distance from $A$ on the sheet. Neglecting gravity, find the time of flight.

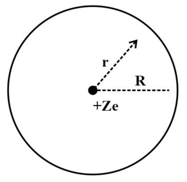
A conducting spherical shell of radius $R$ has a charge $+q$units. The electric field due to the shell at a point

A conducting spherical shell of radius $R$ has a charge $+q$units. The electric field due to the shell at a point

An electron is moving around an infinite linear charge in a circular path of diameter $0.3 \mathrm{m}$. If linear charge density is ${10}^{-6} \mathrm{C}/\mathrm{m}$ and the speed of the electron is written as$n\times {10}^7 \mathrm{m}/\mathrm{s}$, then find $n$ accurate up to two digits after the decimal point. ($m_e=9\times {10}^{-31} \mathrm{kg}$, $e=1.6\times {10}^{-19} \mathrm{C}$)

$\mathrm{A}$ solid conducting sphere of radius $20 \mathrm{cm}$ is enclosed by a thin metallic shell of radius $40 \mathrm{cm}.$ $\mathrm{A}$ charge of $40 \mathrm{\mu C}$ is given to the inner sphere. If the metallic shell is earthed, then the heat generated in the process is

The electric potential at the surface of a charged spherical conductor of radius $10 \mathrm{cm}$ is $15 \mathrm{V}$. Electric potential at its centre in volt is 

An electron of ${10}^{3 }\mathrm{eV}$ energy is fired from a distance of $5 \mathrm{mm}$ perpendicularly towards an infinite charged conducting plate. What should be the minimum charge density on plate so that electron fails to strike the plate?

A particle of mass $9\times {10}^{-5} \mathrm{gm}$ is placed at some height above a uniformly charged horizontal infinite non conducting plate having a surface charge density $5\times {10}^{-5} \mathrm{C}/{\mathrm{m}}^2$. What should be the charge on the particle so that on releasing it will not fall down. Take, $g=9.8 \mathrm{m}/{\mathrm{s}}^2$

Two metallic plates each of area is $1 {\mathrm{m}}^2$ placed parallel to each other at a separation of $0.05 \mathrm{m}$. Both have charges of equal magnitude but of opposite nature. If the magnitude of electric field in space between them is $5.5 \mathrm{V}/\mathrm{m}$, then calculate the magnitude of charge on each plate.

A charge of $10 \mathrm{\mu C}$ is given to a metallic plate of area ${10}^{-2} {\mathrm{m}}^2$. Determine the intensity of electric fields at points near by.

An infinite line charge produces an electric field of $9\times {10}^4 \mathrm{N}/\mathrm{C}$ at $2 \mathrm{cm}$ from it. Determine the linear charge density.

The intensity of electric field due to a charged sphere at a point at a distance of $20 \mathrm{cm}$ from in centre is $10 \mathrm{V}/\mathrm{m}$. The radius of sphere is $5 \mathrm{cm}$. Determine the intensity of electric field at a distance of $8 \mathrm{cm}$ from the centre.

Consider two infinite parallel planes having charge densities $+\sigma$ and $-\sigma$ respectively. What is the magnitude of the electric field at some point in the region between them?

Consider two long straight line charges having linear charge densities ${\lambda }_1$ and ${\lambda }_2$. Derive expression for the force per unit length acting between them.

Graph the variation of electric field with distance for a uniformly charged non-conducting sheet.

Write the expression for force per unit area on a charged spherical conductor and give its direction.

Electric field intensity due to a long straight charged wire varies with $\frac{\mathit{1}}{\mathit{r}}$as shown in 

An early model of an atom considered it to have a positively charged point nucleus of charge $\mathrm{Z}\mathrm{e}$ surrounded by a uniform density of negative charge upto a radius $\mathrm{R}$. The atom as a whole is neutral. The electric field at a distance $\mathrm{r}$ from the nucleus is $(\mathrm{r}<\mathrm{R})$